模拟芯视界 | 用于 PFC 的新型充电模式控制算法

欢迎再次来到我们的技术专栏—— 模拟芯视界 。在上一期中,我们讨论了固定频率 DCS-Control 拓扑的功能和优势。
本次为大家带来的是 《 用于 PFC 的新型充电模式控制算法 》 。该文章将介绍这一算法在实际应用中的表现,以及它如何助力实现更高效、更稳定的电源管理。
引言
在控制系统中,如果您想要控制某个东西,则需要对其进行检测;这也适用于功率因数校正 (PFC) 应用。在功率 >75W 的离线电源中,PFC 控制输入电流以创建正弦波形(换句话说,跟随正弦输入交流电压)。 要控制输入电流,必须对其进行检测。
最常用的电流检测方法是 在 PFC 接地回路放置一个分流电阻器 ( 图 1 中标记为 R)来检测输入电流。检测到的输入电流信号 (I sense ) 随后会被发送到平均电流模式控制器(如 图 2 所示)。由于电流基准 (I REF ) 由输入电压 (V IN ) 调制,因此它是正弦波形。控制环路会强制输入电流跟随 I REF ,从而实现正弦波形。
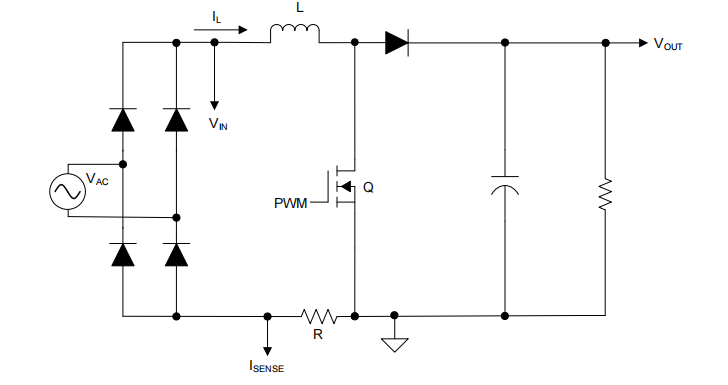
图 1: PFC 的常用电流检测方法
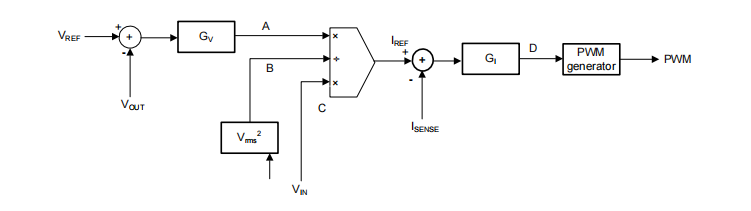
图 2:PFC 的传统平均电流模式控制
几乎所有连续导通模式 (CCM) PFC 控制器都使用传统的平均电流模式控制。 虽然传统的平均电流模式控制可实现良好的功率因数并具有低的总谐波失真,但也 存在一些限制 ,尤其是在图腾柱无桥 PFC 中。 本文介绍了一种全新的控制算法:充电模式控制。
充电模式控制
充电模式控制算法是一个 全新的控制概念: 要控制一个物体,您实际上并不需要对其进行检测—— 您可以 检测其结果,然后间接地控制这个物体。 对于 PFC,该控制算法并不直接控制输入电流,而是 控制每个开关周期中向 PFC 输出提供的电荷量,并采用特殊的控制律,通过控制电荷使得输入电流变为正弦波形。
有几种方法可用于获取电荷信息 。 图 3 显示了使用分流器和运算放大器电路的示例,其中运算放大器配置为积分器。当 PFC 升压开关关断时,电感器电流开始为 PFC 大容量电容器充电。分流电阻器检测此电流,然后电流通过积分器进行积分。积分器输出的峰值表示在每个开关周期中提供给 PFC 输出的总电荷。该电荷 (V charge ) 由控制器作为控制回路反馈信号进行采样。在升压开关关断之前,积分器通过 Q1 放电至零。

图 3:使用分流器和运算放大器来获取电荷信息
图 4 显示了 另一种方法 , 该方法在 PFC 输出侧采用一个电流互感器 (CT)。 CT 输出端连接到电容器 C1。当 PFC 升压开关关断时,电感器电流开始为 PFC 大容量电容器充电。CT 会检测此电流,且其输出会为 C1 充电。C1 上的电压升高;其峰值电压表示传输到 PFC 输出的总电荷。控制器将峰值电压 V CHARGE 作为控制环路反馈信号进行采样。在升压开关关断之前,C1 通过 Q1 放电至 0V。
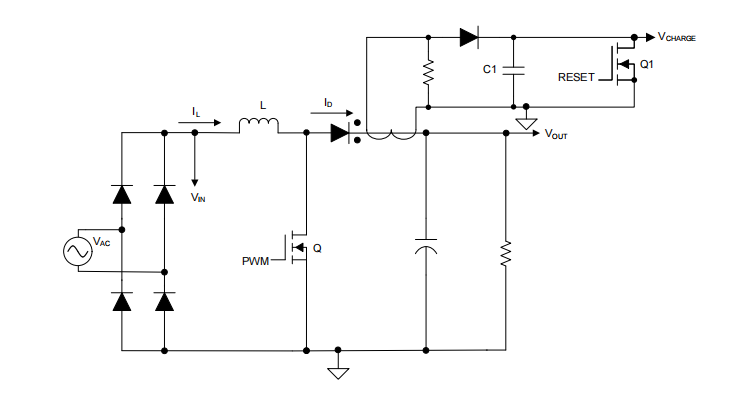
图 4:使用 CT 获取电荷信息
图 5 显示了充电模式控制的典型信号波形。
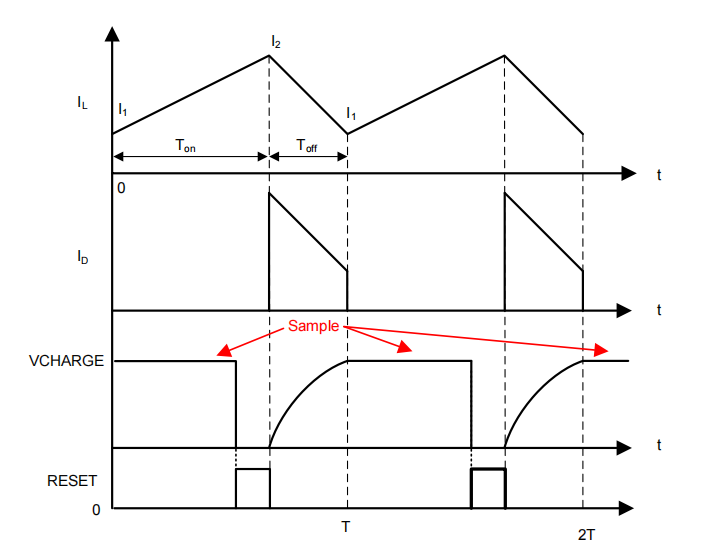
图 5:充电模式控制的典型信号波形
控制律
现在您已经知道如何获得每个开关周期的电荷信息,下面让我们来看看 如何使用新的控制律来获取正弦输入电流波形 ,请参阅 图 6 。
与 图 2 中所示的传统控制律相比, 新控制率有 两个不同之处 :
-
电流回路基准由 V IN 2 调制,而不是由 V IN 调制。
-
反馈信号是电荷 V charge ,而不是 I sense 。

图 6:PFC 的充电模式控制律
在 图 6 中,电流基准 IREF 由以下公式给出:
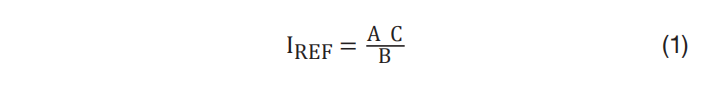
其中,I
REF
是电流环路基准,A 是电压环路输出 G
V
,B 是用于 V
IN
前馈控制的 V
rms
2
,C 是 V
IN
2
。
从 图 5 可以看出, 方程式 2 表示每个开关周期的平均电感器电流为:
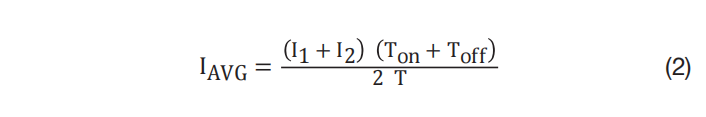
其中,I AVG 是平均电感器电流,I 1 是每个开关周期开始时的电感器电流,I 2 是每个开关周期中的电感器电流峰值,T on 是升压开关 Q 导通时间,T off 是升压二极管 D 导通时间,而 T 是开关周期。
方程式 3 计算每个开关周期中 C1 的峰值电压 (V CHARGE ) 为:
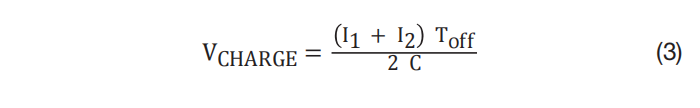
其中,C 为 C1 的电容。
在稳定状态下,控制环路强制 V CHARGE 等于 I REF (请参阅 方程式 4 ):
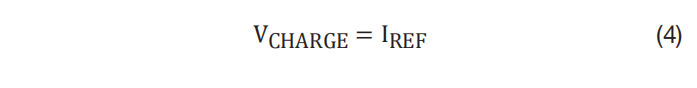
对于稳态运行的升压型转换器,施加到升压电感器上的伏秒必须在每个开关周期中保持平衡(请参阅 方程式 5 ):
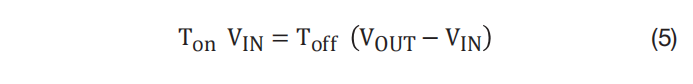
方程式 6 综合了方程式 1 至方程式 5:
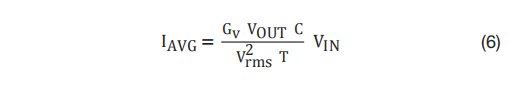
在 方程式 6 中,由于 C 和 T 都是恒定的,并且 G V 、V OUT 和 V rms 2 在稳态下不会变化,因此 I AVG 跟随 V IN 。当 V IN 是正弦波形时,I AVG 也是正弦波形,从而实现 PFC。请注意, 方程式 2 和方程式 3 对于 CCM 和不连续导通模式(DCM) 均有效; 因此, 方程式 6 对于 CCM 和 DCM 运行均有效。
RHPZ 效应和解决方案
当 PFC 以 DCM 模式运行时,充电模式控制的环路补偿很简单。然而, 当升压转换器以 CCM 模式运行时,环路补偿成为了一个挑战, 因为控制环路中会出现一个右半平面零点 (RHPZ)。RHPZ 会导致 相位降幅 ,从而对控制环路的潜在相位裕度产生负面影响。 方程式 7 将控制环路的小信号模型表示为:
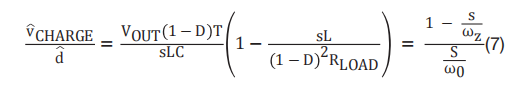
其中 R LOAD 是 PFC 的输出负载,D 是脉宽调制占空比。
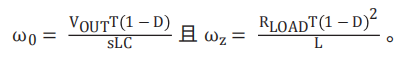
方程式 7 清楚地显示了 RHPZ ωZ 。 其频率随负载、升压电感和 D(D 随输入和输出电压而变化)而变化,这使得环路补偿变得非常困难。
为了消除 RHPZ, 方程式 8 修改了反馈信号:
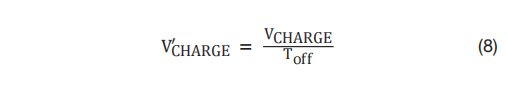
图 7 修改了控制律,其中可以看到 I REF 现在由 V IN 调制, 而不是由 V IN 2 调制。
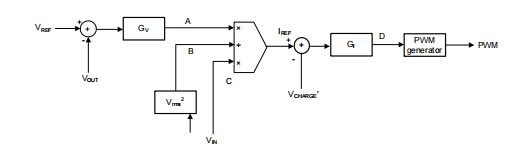
图 7:消除 RHPZ 后 PFC 的充电模式控制律
进行这种修改后, 方程式 9 将控制环路的小信号模型表示为:

RHPZ 消失,并且系统变成一阶系统,因此很容易进行补偿。
图 8 展示了通过仿真来验证新的控制算法,从而实现正弦输入电流波形。

图 8:仿真结果:正弦输入电流波形
结语
充电模式并不是直接控制输入电流,而是控制每个开关周期内向 PFC 输出提供的电荷量。 该算法适用于所有 PFC 拓扑,对于图腾柱无桥 PFC 尤其有用, 因为传统上需要霍尔效应传感器等传感器来检测双向电感器电流。问题在于,霍尔效应传感器不仅价格昂贵 ,还存在带宽有限、对磁场敏感以及直流失调电压随温度而变化等局限性。 由于充电模式控制无需检测电感器电流,因此无需昂贵的双向电流传感器。 相反, 您可以 使用电流检测电阻器以及低带宽运算放大器或 CT,这些的成本要低得多。
由于具有高效率,图腾柱无桥 PFC 非常适合需要高效率的应用。虽然高成本始终是其广泛应用的障碍,但是这种新的控制算法现在是需要高效率和低成本的应用中的一种选择。您可以使用 现有的数字控制器(例如德州仪器 (TI) C2000™ 微控制器和 UCD3138 控制器) 来实现充电模式控制,也可以 在开发新的模拟 PFC 控制器时采用该控制方法。
持续关注我们的专栏,或通过 “阅读原文” 浏览德州仪器 《模拟设计期刊》 电子版 ,一同探索模拟设计的更多可能!






点击 “阅读原文” ,浏览 《模拟设计期刊》电子版, 更多相关知识等待解锁!












 京公网安备 11010802033920号
京公网安备 11010802033920号